Answer:
(a) 0.36
(b) 0.64
(c) 0.53
(d) 0.47
(e) 0.17
(f) 0.77
Explanation:
(a)
Compute the value of P (A₁ ∪ A₂) as follows:
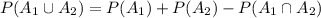
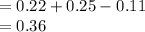
Thus, the value of P (A₁ ∪ A₂) is 0.36.
(b)
Compute the value of P (A₁' ∩ A₂') as follows:
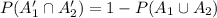
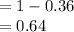
Thus, the value of P (A₁' ∩ A₂') is 0.64.
(c)
Compute the value of P (A₁ ∪ A₂ ∪ A₃) as follows:
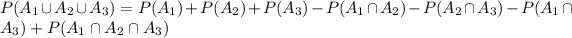
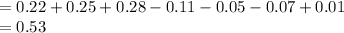
Thus, the value of P (A₁ ∪ A₂ ∪ A₃) is 0.53.
(d)
Compute the value of P (A₁' ∩ A₂' ∩ A'₃) as follows:
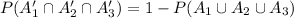
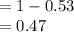
Thus, the value of P (A₁' ∩ A₂' ∩ A'₃) is 0.47.
(e)
Compute the value of P (A₁' ∩ A₂' ∩ A₃) as follows:
![P(A'_(1)\cap A'_(2)\cap A_(3))=P(A_(3))-[P(A_(1)\cap A_(3))+P(A_(2)\cap A_(3))-P(A_(1)\cap A_(2)\cap A_(3))]](https://img.qammunity.org/2021/formulas/mathematics/college/3574y9b2s5zh96s4bozd42irrov8c3eon7.png)
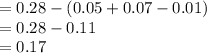
Thus, the value of P (A₁' ∩ A₂' ∩ A₃) is 0.17.
(f)
Compute the value of P ((A₁' ∩ A₂') ∪ A₃) as follows:
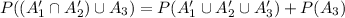
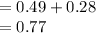
Thus, the value of P ((A₁' ∩ A₂') ∪ A₃) is 0.77.