Question

Point A is at (-7,5) and point C is at (5,-1). Find the coordinates of point B on AC such that AB is 5 times as long as BC.

Answer 1

(3,0)

Explanation:

Answer 2

Point B = (53, -25) satisfies the required condition

Explanation:

Notice that point A is in the second quadrant and point C in the fourth quadrant, and the separation between them in the x-direction is given by:

| 5 - (-7) | = 12

while their separation in the y-direction is:

| -1 -5 | = 6

That means that point C is twelve units to the right and 6 units down from point A. In order to create a segment with another point aligned with them and which has 5 times the length of AC, we then need to consider adding to the x-coordinate of point C 4 times 12 units = 48 units to obtain the x-coordinate of the new point B, and go down 4 times 6 units = 24 units to the y-coordinate of point C.

This is: B = (5+48, -1-24) = (53, -25)

We can verify our procedure by estimating the length of the segment AB and that of segment AC and checking that the first one is indeed 5 times that of AC:

`|AB| =√((53-(-7))^2+(-25-5)^2) = √(3600+900) =√(4500) =√(2^2\,3^2\,5^3) =5\,√(180)`

`|AC| =√((5-(-7))^2+(-1-5)^2) = √(144+36) =√(180)`

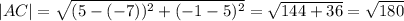
Therefore this new point B is indeed giving as a segment of the desired length.