Answer:
The probability that a randomly selected call time will be less than 30 seconds is 0.7443.
Explanation:
We are given that the caller times at a customer service center has an exponential distribution with an average of 22 seconds.
Let X = caller times at a customer service center
The probability distribution (pdf) of the exponential distribution is given by;

Here,
 = exponential parameter
= exponential parameter
Now, the mean of the exponential distribution is given by;
Mean =
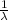
So,
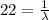 ⇒
⇒
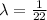
SO, X ~ Exp(
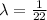 )
)
To find the given probability we will use cumulative distribution function (cdf) of the exponential distribution, i.e;
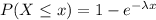 ; x > 0
; x > 0
Now, the probability that a randomly selected call time will be less than 30 seconds is given by = P(X < 30 seconds)
P(X < 30) =

= 1 - 0.2557
= 0.7443