Question

Pleaseeee help❤️I would appreciate itttt

Answer 1

The correct option are;

i) The line segment must connect an _1_ (open) circle at point B to an _1_ (open) circle at point D.

ii) The line segment must connect an _1_ (open) circle at point B to a _2_ (closed) circle at point C

Explanation:

The parameters given are;

Domain:
`\-4<x\leq 4, x \in R \`

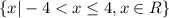
Range:
`\-4\leq y< 4, y \in R \`

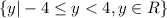
Given that to indicate less than (<) on a graph of an inequality, we draw an circle over the point in reference while to indicate less than or equal to (≤) we draw an circle over the point in reference and shade the point, therefore we have;

Given that x > -4, and ≤ 4, the points B and C satisfies the conditions

Given that the y-coordinates are y ≥ -4, and y < 4, the points D and C satisfies the conditions

Where:

Point B = (4, 4) satisfies x only

Point C = (4, -4) satisfies x and y

Point D = (-4, -4) satisfies y only

Therefore, in order to draw a line segment between two points;

i) The line segment must connect an _1_ (open) circle at point B to an _1_ (open) circle at point D.

ii) The line segment must connect an _1_ (open) circle at point B to a _2_ (closed) circle at point C.