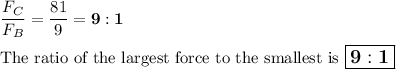Question

I NEED HELP PLEASE, THANKS! :)

Three positive charges A, B, and C, and a negative charge D are placed in a line as shown in the diagram. All four charges are of equal magnitude. The distances between A and B, B and C, and C and D are equal.
a. Which charge experiences the greatest net force? Which charge experiences the smallest net force?
b. Find the ratio of the greatest to the smallest net force.

Answer 1

1. Largest force: C; smallest force: B; 2. ratio = 9:1

Step-by-step explanation:

The formula for the force exerted between two charges is

`F=K( q_(1)q_(2))/(r^(2))`

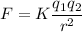
where K is the Coulomb constant.

q₁ and q₂ are also identical and constant, so Kq₁q₂ is also constant.

For simplicity, let's combine Kq₁q₂ into a single constant, k.

Then, we can write

`F=(k)/(r^(2))`

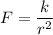
1. Net force on each particle

Let's

• Call the distance between adjacent charges d.
• Remember that like charges repel and unlike charges attract.

Define forces exerted to the right as positive and those to the left as negative.

(a) Force on A

`\begin{array}{rcl}F_(A) & = & F_(B) + F_(C) + F_(D)\\& = & -(k)/(d^(2)) - (k)/((2d)^(2)) +(k)/((3d)^(2))\\& = & (k)/(d^(2))\left(-1 - (1)/(4) + (1)/(9) \right)\\\\& = & (k)/(d^(2))\left((-36 - 9 + 4)/(36) \right)\\\\& = & \mathbf{-(41)/(36) (k)/(d^(2))}\\\\\end{array}`

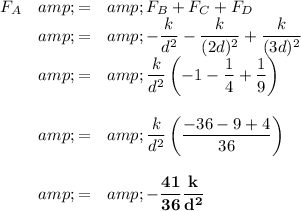
(b) Force on B

`\begin{array}{rcl}F_(B) & = & F_(A) + F_(C) + F_(D)\\& = & (k)/(d^(2)) - (k)/(d^(2)) + (k)/((2d)^(2))\\& = & (k)/(d^(2))\left((1)/(4) \right)\\\\& = &\mathbf{(1)/(4) (k)/(d^(2))}\\\\\end{array}`

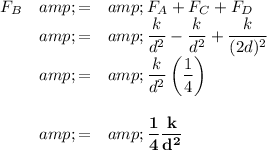
(C) Force on C

`\begin{array}{rcl}F_(C) & = & F_(A) + F_(B) + F_(D)\\& = & (k)/((2d)^(2)) + (k)/(d^(2)) + (k)/(d^(2))\\& = & (k)/(d^(2))\left( (1)/(4) +1 + 1 \right)\\\\& = & (k)/(d^(2))\left((1 + 4 + 4)/(4) \right)\\\\& = & \mathbf{(9)/(4) (k)/(d^(2))}\\\\\end{array}`

(d) Force on D

`\begin{array}{rcl}F_(D) & = & F_(A) + F_(B) + F_(C)\\& = & -(k)/((3d)^(2)) - (k)/((2d)^(2)) - (k)/(d^(2))\\& = & (k)/(d^(2))\left( -(1)/(9) - (1)/(4) -1 \right)\\\\& = & (k)/(d^(2))\left((-4 - 9 -36)/(36) \right)\\\\& = & \mathbf{-(49)/(36) (k)/(d^(2))}\\\\\end{array}`

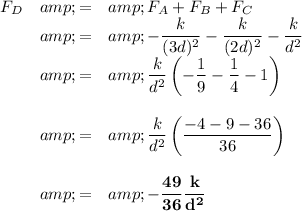
(e) Relative net forces

In comparing net forces, we are interested in their magnitude, not their direction (sign), so we use their absolute values.

`F_(A) : F_(B) : F_(C) : F_(D) = (41)/(36) : (1)/(4) : (9)/(4) : (49)/(36)\ = 41 : 9 : 81 : 49\\\\\text{C experiences the largest net force.}\\\text{B experiences the smallest net force.}\\`

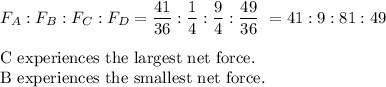
2. Ratio of largest force to smallest

`( F_(C))/( F_(B)) = (81)/(9) = \mathbf{9:1}\\\\\text{The ratio of the largest force to the smallest is $\large \boxed{\mathbf{9:1}}$}`