Question

Draw an angle and then draw the opposite ray to one of its sides, to form a linear pair. Find the measure of the angle formed by the angle bisector of the original angle and the opposite ray if the original angle measures 50°, 90°, and 150°. 1. If the angle equals 50°, then the measurement of the required angle is ? 2. If the angle equals 90°, then the measurement of the required angle is ? 3. If the angle equals 150°, then the measurement of the required angle is ?

Answer 1

(1)155 degrees

(2)135 degrees

(3)105 degrees

Explanation:

Let the original angle
`= \theta`

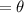
Angle Bisector of the original angle =
`( \theta)/(2)`

If the other angle forms a linear pair, then:

The other angle,
`\beta=180^\circ-\theta`

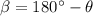
Therefore, the measure of the angle formed by the angle bisector of the original angle and the opposite ray is:

`( \theta)/(2)+180^\circ-\theta\\=180^\circ-( \theta)/(2)`

(1)If the angle equals 50°

Then the measurement of the required angle

`=180^\circ-( 50)/(2)\\=180^\circ-25^\circ\\=155^\circ`

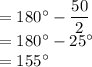
(2)If the angle equals 90°

Then the measurement of the required angle

`=180^\circ-( 90)/(2)\\=180^\circ-45^\circ\\=135^\circ`

{3)If the angle equals 150°

Then the measurement of the required angle

`=180^\circ-( 150)/(2)\\=180^\circ-75^\circ\\=105^\circ`

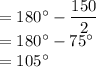
See attachment for an example of the graphical solution.