Answer:
A sample of 601 bricks will be needed.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
The margin of error is:
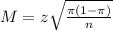
95% confidence level
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
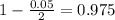 , so
, so
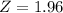 .
.
How large a sample will we need?
A sample of n bricks will be needed.
n is found when M = 0.04.
We have no estimate for the proportion of defective bricks, so we work with the worst case scenario, which is
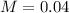
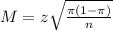
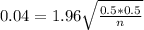
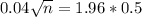
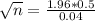

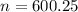
Rounding up
A sample of 601 bricks will be needed.