Answer:
Problem 2):
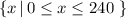
which agrees with answer C listed.
Problem 3) : D = (-3, 6] and R = [-5, 7]
which agrees with answer D listed
Explanation:
Problem 2)
The Domain is the set of real numbers in which the function (given by a graph in this case) is defined. We see from the graph that the line is defined for all x values between 0 and 240. Such set, expressed in "set builder notation" is:

Problem 3)
notice that the function contains information on the end points to specify which end-point should be included and which one should not. The one on the left (for x = -3 is an open dot, indicating that it should not be included in the function's definition, therefor the Domain starts at values of x strictly larger than -3. So we use the "parenthesis" delimiter in the interval notation for this end-point. On the other hand, the end point on the right is a solid dot, indicating that it should be included in the function's definition, then we use the "square bracket notation for that end-point when writing the Domain set in interval notation:
Domain = (-3, 6]
For the Range (the set of all those y-values connected to points in the Domain) we use the interval notation form:
Range = [-5, 7]
since there minimum y-value observed for the function is at -5 , and the maximum is at 7, with a continuum in between.