Question

I NEED HELP PLEASE, THANKS! :)

Three positive charges A, B, and C, and a negative charge D are placed in a line as shown in the diagram. All four charges are of equal magnitude. The distances between A and B, B and C, and C and D are equal.
a. Which charge experiences the greatest net force? Which charge experiences the smallest net force?
b. Find the ratio of the greatest to the smallest net force.

Answer 1

charge C = greatest net force

charge B = the smallest net force

ratio = 9 : 1

Step-by-step explanation:

we know that in Electrostatic Forces, when 2 charges are at same sign then they repel each other and if they are different signed charges then they attract each other

so as per Coulomb's formula of Electrostatic Forces

F =
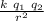`(k\ q_1\ q_2)/(r^2)` .....................1

and here k is 9 ×
`10^9` N.m²/c² and we consider each charge at distance d

so two charge force at A to B is

F1 =
`(k\ q^2)/(d^2)`

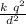
and force between charges at A to C, at 2d distance

F1 =
`(k\ q^2)/((2d)^2)` =
`(k\ q^2)/(4d^2)`

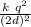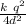
force between charges at A to D, 3d distance

F1 =
`(k\ q^2)/((3d)^2)` =
`(k\ q^2)/(9d^2)`

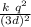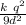
so

Charge a It receives force to the left from b and c and to the right from d

so at a will be

F(a) = -F1 - F2 + F3 ....................2

put here value

F(a) =
`-(k\ Q^2)/(d^2)-(k\ Q^2)/(4d^2)+(k\ Q^2)/(9d^2)`

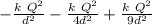
solve it

F(a) =
`(k\ q^2)/(d^2)(-1-(1)/(4)+(1)/(9))`

F(a) =
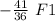`-(41)/(36)\ F1` = 1.13 F1

and

Charge b It receives force to the right from a and d and to the left from c

F(b) = F1 - F1 + F2 ....................3

F(b) =
`(k\ q^2)/(d^2)-(k\ q^2)/(d^2)+(k\ q^2)/(4d^2)`

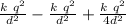
F(b) =
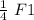`(1)/(4) \ F1` = 0.25 F1

and

Charge c It receives forces to the right from all charges.

F(c) = F2 + F 1 + F 1 ....................4

F(c) =
`(k\ q^2)/(4d^2)+(k\ q^2)/(d^2)+(k\ q^2)/(d^2)`

F(c) =
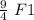`(9)/(4) \ F1` = 2.25 F1

and

Charge d It receives forces to the left from all charges

F(d) = - F3 - F2 -F 1 ....................5

F(d) =
`-(k\ q^2)/(9d^2)-(k\ q^2)/(4d^2)-(k\ q^2)/(d^2)`

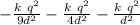
so

F(d) =
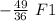`-(49)/(36) \ F1` = 1.36 F1

and

now we get here ratio of the greatest to the smallest net force that is

ratio =
`(2.25)/(0.25)`

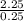
ratio = 9 : 1