Question

What is the center of a circle represented by the equation (x+9Mrs. Culland is finding the center of a circle whose equation is x2 + y2 + 6x + 4y – 3 = 0 by completing the square. Her work is shown.

x2 + y2 + 6x + 4y – 3 = 0

x2 + 6x + y2 + 4y – 3 = 0

(x2 + 6x) + (y2 + 4y) = 3

(x2 + 6x + 9) + (y2 + 4y + 4) = 3 + 9 + 4)2+(y−6)2=102?

Answer 1

The center of the circle is at the point (-3, -2) on the plane

Explanation:

The first four steps in the completing of the squares to find the standard equation of a circle are correct. Let's start from there and actually complete the squares correctly:

`(x^2+6\,x+9)+(y^2+4\,y+4)=3+9+4\\(x+3)^2+(y+2)^2=16\\(x+3)^2+(y+2)^2=4^2`

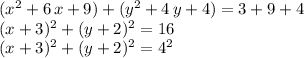
Therefore, this is a circle centered at x = -3 [based on the horizontal translation defined by (x+3)], and at y = -2 [based on the vertical translation defined by (y+2)], and the circle has radius 4 based on the numerical constant squared on the right side of the equal sign.