Question

In parallelogram ABCD, AB = 16 cm, DA = 3
`√(2)` cm, and sides AB and DA form a 45-degree interior angle. In isosceles trapezoid WXYZ with WX ≠ YZ, segment WX is the longer parallel side and has length 16 cm, and two interior angles each have a measure of 45 degrees. Trapezoid WXYZ has the same area as parallelogram ABCD. What is the length of segment YZ?

Answer 1

8

Explanation:

YZ = 8

Answer 2

length of segment YZ is 8 cm

Explanation:

given data

AB = 16 cm

DA = 3
`√(2)` cm

AB and DA form interior angle = 45-degre

WX ≠ YZ

WX = 16 cm

to find out

length of segment YZ

solution

area of △ABD is the same as the area of △BCD

and

area of △ABD is express as

area of △ABD = AB × AD × sin(45) ÷ 2 ............1

put here value

area of △ABD = 16 × 3√2 × sin(45) ÷ 2

area of △ABD = 24

and

area of the parallelogram is

area of the parallelogram = 24 × 2

area of the parallelogram = 48

so

now we will consider here YZ = x

and Since ZY XW is isosceles trapezoid

so here we can say that

WM = ZM = (16 - x) ÷ 2 .......................2

so area of trapezoid will be

area of trapezoid =
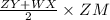`(ZY + WX )/(2) * ZM` .......................3

area of trapezoid =
`(x+16)/(2) * (16 - x)/(2)`

48 =
`(x+16)/(2) * (16 - x)/(2)`

solve it we get

x = 8

so length of segment YZ is 8 cm