Question

A wall is in the shape of a trapezium. The first level of the wall is made up of 50 bricks where as the top level has 14 bricks. If the levels differ from each other by 4 bricks, determine the number of;

(i)levels of the bricks.
(ii)bricks used to make the wall.​

Answer 1

i). 10 levels of the bricks

ii). 320 bricks

Explanation:

First level contains number of bricks = 50

Second level will contain = 50 - 4 = 46 bricks

Similarly, 3rd level will contain number of bricks = 46 - 4 = 42

Therefore, sequence formed for the number of bricks in each level of the wall will be,

50, 46, 42........14

This sequence is an arithmetic sequence having,

First term 'a' = 50

Common difference 'd' = 46 - 50 = (-4)

Last term of the sequence
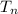`T_(n)`= 14

i). Expression representing last term will be,

`T_(n)=a+(n-1)d`

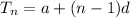
Here
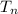`T_(n)` = nth term

a = first term

n = number of term (Number of level of the wall)

d = common difference

By substituting these values in the formula,

14 = 50 + (n - 1)(-4)

14 - 50 = (-4)(n - 1)

-36 = -4(n - 1)

9 = (n - 1)

n = 9 + 1

n = 10

ii). Number of bricks used in the wall = Sum of the sequence

Expression for the sum of an arithmetic sequence is,

`S_n=(n)/(2)[2a+(n-1)d]`

`S_n=(10)/(2)[2* 50+(10-1)(-4)]`

= 5(100 - 36)

= 320 bricks