Question

Major arc JL measures 300°. Circle M is shown. Line segments M J and M L are radii. Tangents J K and L K intersect at point K outside of the circle. Major arc J L is 300 degrees. Which describes triangle JLM? right obtuse scalene equilateral

Answer 1

d

Explanation:

on edge 2020

Answer 2

Equilateral triangle

Explanation:

Given question is incomplete; find the figure for this question attached.

From the figure attached,

A circle M has been given with line segments MJ and ML as radii.

MJ ≅ ML

m(major arc JL) = 300°

Therefore,
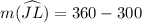`m(\widehat{JL})=360-300` = 60°

And the angle subtended by the arc JL at the center = 60°

m∠JML = 60°

Now in ΔJML,

m(∠JML) + m(∠JLM) + m(∠LJM) = 180°

m(∠JML) + m(∠LJM) + m(∠LJM) = 180°

[m(∠JLM) = m(∠LJM) Opposite angles of radii of a circle measure equal]

60° + 2m(∠LJM) = 180°

m(∠LJM) =
`(180-60)/(2)` = 60°

Therefore, m(∠LJM) = m(∠JML) = m(∠JLM) = 60°

ΔJLM will be an equilateral triangle.