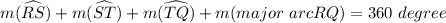Question

I rlly rlly rlly need help! Complete the following proof. Given: Points R, S, T, Q on circle O Prove: m\overarc RS + m\overarc ST + m\overarc TQ + m\overarc RQ

Answer 1

`m(\widehat {RS})+m(\widehat{ST})+m(\widehat{TQ}) + m(major\ arc RQ) = 360\ degree`

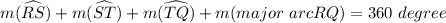
Explanation:

As we can see in the figure that

The R, S, T ,and Q are the points on the circle O.

Also

The measurement of the circular arc is equivalent to the measurement of the angle at the center of the arc

So by this

`m(\widehat{RS})=m(\angle ROS)`

`m(\widehat{ST})=m(\angle SOT)`

`m(\widehat{TQ})=m(\angle TOQ)`

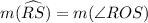
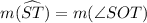
m(major arc RQ) = m(∠QOR)

So,

`m(\widehat {RS})+m(\widehat{ST})+m(\widehat{TQ}) + m(major\ arc RQ) = m(\angle ROS)+m(\angle SOT)+m(\angle TOQ)+m(\angle QOR)`

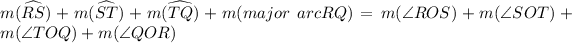
And as we know that

All angles sum = 360°

Therefore

`m(\widehat {RS})+m(\widehat{ST})+m(\widehat{TQ}) + m(major\ arc RQ) = 360\ degree`