Question

In circle P, diameter QS measures 20 centimeters. Circle P is shown. Line segment Q S is a diameter. Line segment R P is a radius. Angle R P S is 123 degrees. What is the approximate length of arc QR? Round to the nearest tenth of a centimeter. 9.9 centimeters 19.9 centimeters 21.5 centimeters 43.0 centimeters

Answer 1

9.9 cm

Explanation:

Answer 2

Length of arc QR is
`\approx` 9.9 cm

Explanation:

Given that circle P, i.e. center is point P.

QS is diameter with length 20 cm.

Given that RP is the radius with

`\angle RPS = 123^\circ`

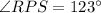
To find length of arc QR = ?

Solution:

Arc QR subtends the
`\angle QPR` on center P.

So, we need to find the angle
`\angle QPR` to find the length of arc QR.

QS is the diameter so
`\angle QPS = 180^\circ`

`\angle QPS = 180^\circ = \angle QPR +\angle RPS\\\Rightarrow 180^\circ = \angle QPR +123^\circ\\\Rightarrow \angle QPR = 57^\circ`

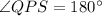
Converting in radians,

`\angle QPR = 57^\circ * (\pi)/(180) = 0.99\ radians`

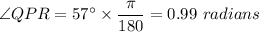
Using the formula for length of arc:

`l = \theta * R`

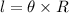
Where
`\theta` is the angle subtended by the arc on center.

R is the radius of circle.

Here,

`\theta = 0.99\ radians\\R = 10\ cm`

`l = 0.99 * 10\\l = 9.9\ cm`

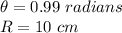
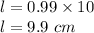
Length of arc QR is
`\approx` 9.9 cm