Answer:
m = 57/14 =
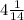
Explanation:
The polynomial can be expressed as follows;
P(x) = 2·x³ - m·x² + x - 5·m
(2·x³ - m·x² + x - 5·m) ÷ (x - 2)
2·x²
(-m - 2)·x² + x
(-m - 2)·x
(m + 3)·x - 5·m
(m + 3)·x
-5·m
The remainder = -5·m/(x -2)
Similarly, dividing by (x + 1) will give a remainder of -5·m/(x + 1)
But -5·m/(x -2) = 4×-5·m/(x + 1)
5/(x -2) = 20/(x + 1)
5(x + 1) = 20(x -2)
20x - 5x= 40 + 5
x = 45/15 = 3
2·3³ - m·3² + 3 - 5·m = 54 - 9m + 3 - 5m = 57 - 14m
(57 - 14m)/1 = (57 - 14m)/4
228 - 56m =57 - 14m
171 = 56m-14m = 42m
m = 171/42 = 57/14.