Question

A nozzle receives an ideal gas flow with a velocity of 25 m/s, and the exit at 100 kPa, 300 K velocity is 250 m/s. Determine the inlet temperature if the gas is argon, helium, or nitrogen.

Answer 1

Given Information:

Inlet velocity = Vin = 25 m/s

Exit velocity = Vout = 250 m/s

Exit Temperature = Tout = 300K

Exit Pressure = Pout = 100 kPa

Required Information:

Inlet Temperature of argon = ?

Inlet Temperature of helium = ?

Inlet Temperature of nitrogen = ?

Answer:

Inlet Temperature of argon = 360K

Inlet Temperature of helium = 306K

Inlet Temperature of nitrogen = 330K

Step-by-step explanation:

Recall that the energy equation is given by

`$ C_p(T_(in) - T_(out)) = (1)/(2) * (V_(out)^2 - V_(in)^2) $`

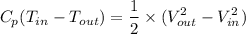
Where Cp is the specific heat constant of the gas.

Re-arranging the equation for inlet temperature

`$ T_(in) = (1)/(2) * ((V_(out)^2 - V_(in)^2))/(C_p) + T_(out)$`

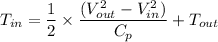
For Argon Gas:

The specific heat constant of argon is given by (from ideal gas properties table)

`C_p = 520 \:\: J/kg.K`

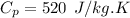
So, the inlet temperature of argon is

`$ T_(in) = (1)/(2) * ((250^2 - 25^2))/(520) + 300$`

`$ T_(in) = (1)/(2) * 119 + 300$`

`$ T_(in) = 360K $`

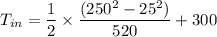
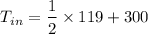
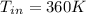
For Helium Gas:

The specific heat constant of helium is given by (from ideal gas properties table)

`C_p = 5193 \:\: J/kg.K`

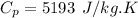
So, the inlet temperature of helium is

`$ T_(in) = (1)/(2) * ((250^2 - 25^2))/(5193) + 300$`

`$ T_(in) = (1)/(2) * 12 + 300$`

`$ T_(in) = 306K $`

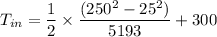
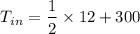
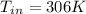
For Nitrogen Gas:

The specific heat constant of nitrogen is given by (from ideal gas properties table)

`C_p = 1039 \:\: J/kg.K`

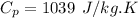
So, the inlet temperature of nitrogen is

`$ T_(in) = (1)/(2) * ((250^2 - 25^2))/(1039) + 300$`

`$ T_(in) = (1)/(2) * 60 + 300$`

`$ T_(in) = 330K $`

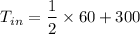
Note: Answers are rounded to the nearest whole numbers.