Question

A 95% confidence interval for a population mean is determined to be 100 to 120. If the confidence coefficient is reduced to 0.90, the interval:_________ a. becomes narrower b. becomes wider c. does not change d. becomes 0.1

Answer 1

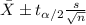`\bar X \pm t_(\alpha/2)(s)/(√(n))` (1)

The confidence interval for this case would be:

`100 \leq \mu \leq 120`

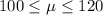
And we want to know what happens with the interval if we reduce the confidence level to 90% and for this case we will get a narrower interval since the critical value
`t_(\alpha/2)` would be lower. So then the best option would be:

a. becomes narrower

Explanation:

Notation

`\bar X` represent the sample mean for the sample

`\mu` population mean

s represent the sample standard deviation

n represent the sample size

Solution

The confidence interval for the mean is given by the following formula:

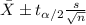`\bar X \pm t_(\alpha/2)(s)/(√(n))` (1)

The confidence interval for this case would be:

`100 \leq \mu \leq 120`

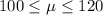
And we want to know what happens with the interval if we reduce the confidence level to 90% and for this case we will get a narrower interval since the critical value
`t_(\alpha/2)` would be lower. So then the best option would be:

a. becomes narrower