Answer:
Apparently
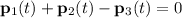 .
.
One possible basis for this span is
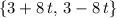 .
.
Explanation:
Linear Dependence
A set of vectors is linearly-dependent if one of the vectors is a linear combination of the others.
Alternatively, to show linear dependence, show that the equation
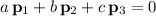 has a non-trivial solution (where at least one of the three scalars
has a non-trivial solution (where at least one of the three scalars
 ,
,
 , and
, and
 is non-zero.)
is non-zero.)
For this set of polynomials, it can be shown that:
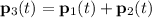 , or equivalently,
, or equivalently,
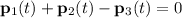 .
.
Either way, the set
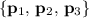 would be linearly-dependent.
would be linearly-dependent.
Basis of the Span
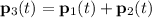 implies that
implies that
 is a linear combination of
is a linear combination of
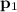 and
and
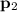 . Therefore,
. Therefore,
 is in the span of
is in the span of
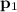 and
and
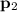 (in other words,
(in other words,
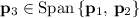 .) Hence:
.) Hence:
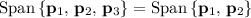 .
.
Therefore, any basis of the set
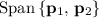 would also be a basis of the set
would also be a basis of the set
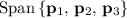 .
.
On the other hand, it can be shown that
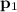 and
and
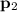 are linearly-independent. Therefore,
are linearly-independent. Therefore,
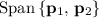 should have a dimension of
should have a dimension of
 . As a result, there should be exactly
. As a result, there should be exactly
 linearly-independent vectors in a basis of
linearly-independent vectors in a basis of
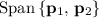 .
.
There are many different choices for the basis of
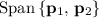 . One possible choice is the set
. One possible choice is the set
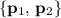 , which is equal to
, which is equal to
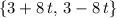 . Make sure that this set is indeed linearly-independent and contains two vectors.
. Make sure that this set is indeed linearly-independent and contains two vectors.
Because it has already been shown that
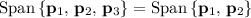 ,
,
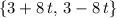 should be a basis of the set
should be a basis of the set
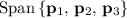 , as well.
, as well.