Question

A Rankine steam power plant is considered. Saturated water vapor enters a turbine at 8 MPa and exits at condenser at 10 kPa. The pump is considered isentropic and the turbine isentropic efficiency is 85%. If the net power output is 100 MW calculate the thermal efficiency of the plant and the mass flow rate of steam

Answer 1

0.31

126.23 kg/s

Step-by-step explanation:

Given:-

- Fluid: Water

- Turbine: P3 = 8MPa , P4 = 10 KPa , nt = 85%

- Pump: Isentropic

- Net cycle-work output, Wnet = 100 MW

Find:-

- The thermal efficiency of the cycle

- The mass flow rate of steam

Solution:-

- The best way to deal with questions related to power cycles is to determine the process and write down the requisite properties of the fluid at each state.

First process: Isentropic compression by pump

P1 = P4 = 10 KPa ( condenser and pump inlet is usually equal )

h1 = h-P1 = 191.81 KJ/kg ( saturated liquid assumption )

s1 = s-P1 = 0.6492 KJ/kg.K

v1 = v-P1 = 0.001010 m^3 / kg

P2 = P3 = 8 MPa( Boiler pressure - Turbine inlet )

s2 = s1 = 0.6492 KJ/kg.K .... ( compressed liquid )

- To determine the ( h2 ) at state point 2 : Pump exit. We need to determine the wok-done by pump on the water ( Wp ). So from work-done principle we have:

`w_p = v_1*( P_2 - P_1 )\\\\w_p = 0.001010*( 8000 - 10 )\\\\w_p = 8.0699 (KJ)/(kg)`

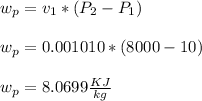
- From the following relation we can determine ( h2 ) as follows:

h2 = h1 + wp

h2 = 191.81 + 8.0699

h2 = 199.88 KJ/kg

Second Process: Boiler supplies heat to the fluid and vaporize

- We have already evaluated the inlet fluid properties to the boiler ( pump exit property ).

- To determine the exit property of the fluid when the fluid is vaporized to steam in boiler ( super-heated phase ).

P3 = 8 MPa

T3 = ? ( assume fluid exist in the saturated vapor phase )

h3 = hg-P3 = 2758.7 KJ/kg

s3 = sg-P3 = 5.7450 KJ/kg.K

- The amount of heat supplied by the boiler per kg of fluid to the water stream. ( qs ) is determined using the state points 2 and 3 as follows:

`q_s = h_3 - h_2\\\\q_s = 2758.7 -199.88\\\\q_s = 2558.82 (KJ)/(kg)`

Third Process: The expansion ( actual case ). Turbine isentropic efficiency ( nt ).

- The saturated vapor steam is expanded by the turbine to the condenser pressure. The turbine inlet pressure conditions are similar to the boiler conditions.

- Under the isentropic conditions the steam exits the turbine at the following conditions:

P4 = 10 KPa

s4 = s3 = 5.7450 KJ/kg.K ... ( liquid - vapor mixture phase )

- Compute the quality of the mixture at condenser inlet by the following relation:

`x = (s_4 - s_f)/(s_f_g) \\\\x = (5.745- 0.6492)/(7.4996) \\\\x = 0.67947`

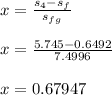
- Determine the isentropic ( h4s ) at this state as follows:

`h_4_s = h_f + x*h_f_g\\\\h_4_s = 191.81 + 0.67947*2392.1\\\\h_4_s = 1817.170187 (KJ)/(kg)`

- Since, we know that the turbine is not 100% isentropic. We will use the working efficiency and determine the actual ( h4 ) at the condenser inlet state:

`h4 = h_3 - n_t*(h_3 - h_4_s ) \\\\h4 = 2758.7 - 0.85*(2758.7 - 181.170187 ) \\\\h4 = 1958.39965 (KJ)/(kg) \\`

- We can now compute the work-produced ( wt ) due to the expansion of steam in turbine.

`w_t = h_3 - h_4\\\\w_t = 2758.7-1958.39965\\\\w_t = 800.30034 (KJ)/(kg)`

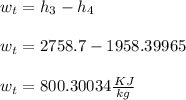
- The net power out-put from the plant is derived from the net work produced by the compression and expansion process in pump and turbine, respectively.

`W_n_e_t = flow(m) * ( w_t - w_p )\\\\flow ( m ) = (W_n_e_t)/(w_t - w_p) \\\\flow ( m ) = (100000)/(800.30034-8.0699) \\\\flow ( m ) = 126.23 (kg)/(s)`

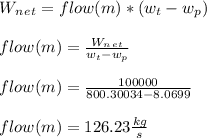
Answer: The mass flow rate of the steam would be 126.23 kg/s

- The thermal efficiency of the cycle ( nth ) is defined as the ratio of net work produced by the cycle ( Wnet ) and the heat supplied by the boiler to the water ( Qs ):

`n_t_h = (W_n_e_t)/(flow(m)*q_s) \\\\n_t_h = (100000)/(126.23*2558.82) \\\\n_t_h = 0.31`

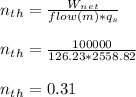
Answer: The thermal efficiency of the cycle is 0.31