Question

Assume a​ Cobb-Douglas production function of the​ form: q equals 10 Upper L Superscript 0.33 Baseline Upper K Superscript 0.75. What type of returns to scaleLOADING... does this production function​ exhibit?

Answer 1

Since 0.33 + 0.75 = 1.08 is greater than one, this production function therefore exhibits increasing returns to scale.

Step-by-step explanation:

From the question, we have the following restated equation:

`q=10L^(0.33) K^(0.75)`

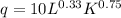
Where q is the output, and L and K are inputs

To determine the types of returns to scale, we increase each of L and K inputs by constant amount c as follows:

`q = 10(cL)^(0.33)(cK)^(0.75)`

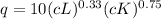
We can now solve as follows;

`q = 10c^(0.33+0.75) L^(0.33)K^(0.75)`

`q=c^(1.08) L^(0.33) K^(0.75)`

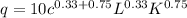
Since 0.33 + 0.75 = 1.08 is greater than one, this production function therefore exhibits increasing returns to scale.