Answer: 3.712 hours or more
Explanation:
Let X be the random variable that denotes the time required to complete a product.
X is normally distributed.
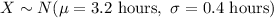
Let x be the times it takes to complete a random unit in order to be in the top 10% (right tail) of the time distribution.
Then,

![P(z>(x-3.2)/(\sigma))=0.10\ \ \ [z=(x-\mu)/(\sigma)]](https://img.qammunity.org/2021/formulas/mathematics/college/ebap9t4jiquu4b7pba4ybcyu7wancin5zy.png)
As,
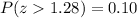 [By z-table]
[By z-table]
Then,
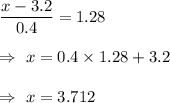
So, it will take 3.712 hours or more to complete a random unit in order to be in the top 10% (right tail) of the time distribution.