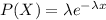Answer:

But also we can define the variable in terms of
 like this:
like this:
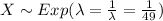
And usually this notation is better since the probability density function is defined as:
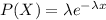
Explanation:
We know that the random variable X who represents the waiting time to see a shooting star during a meteor shower follows an exponential distribution and for this case we can write this as:

But also we can define the variable in terms of
 like this:
like this:
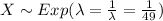
And usually this notation is better since the probability density function is defined as: