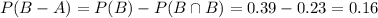Question

In a certain town 56% of the households own mutual funds, 39% own individual stocks, and 23% own both. What is the percentage of households that own individual stocks but not mutual funds?

Answer 1

A= the households own mutual funds

B= the household own individual stocks

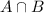`A \cap B` the household own both

And we know the following probabilities:

`P(A)= 0.56, P(B)= 0.39, P(A \cap B) = 0.23`

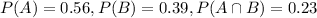
For this case we want to find this probability:

households that own individual stocks but not mutual funds

And we can find this with:

`P(B-A) =P(B) -P(B \cap B)`

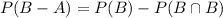
And replacing we got:

`P(B-A) =P(B) -P(B \cap B)=0.39-0.23= 0.16`

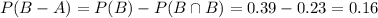
Explanation:

For this problem we can define the following notation:

A= the households own mutual funds

B= the household own individual stocks

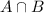`A \cap B` the household own both

And we know the following probabilities:

`P(A)= 0.56, P(B)= 0.39, P(A \cap B) = 0.23`

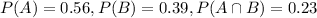
For this case we want to find this probability:

households that own individual stocks but not mutual funds

And we can find this with:

`P(B-A) =P(B) -P(B \cap B)`

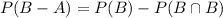
And replacing we got:

`P(B-A) =P(B) -P(B \cap B)=0.39-0.23= 0.16`