Question

A piece of wire of length 7070 is​ cut, and the resulting two pieces are formed to make a circle and a square. Where should the wire be cut to​ (a) minimize and​ (b) maximize the combined area of the circle and the​ square?

Answer 1

a.x=39.2

b.Use whole wire as a circle

Explanation:

We are given that

Length of piece of wire=70 units

Let length of wire used to make a square =x units

Length of wire used in circle=70- x

Side of square=
`(perimeter\;of\;square)/(4)=(x)/(4)`

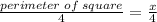
Circumference of circle=
`2\pi r`

`70-x=2\pi r`

`r=(70-x)/(2\pi)`

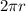
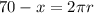
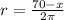
Combined area of circle and square,A=
`((x)/(4))^2+\pi((70-x)/(2\pi))^2`

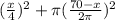
Using the formula

Area of circle=
`\pi r^2`

Area of square=
`(side)^2`

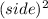
a.
`A=(x^2)/(16)+(4900+x^2-140x)/(4\pi)`

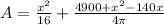
Differentiate w.r.t x

`(dA)/(dx)=(x)/(8)+(2x-140)/(4\pi)`

`(dA)/(dx)=0`

`(x)/(8)+(2x-140)/(4\pi)=0`

`(\pi x+4x-280)/(4\pi)=0`

`\pi x+4x-280=0`

`x(\pi+4)=280`

`x=(280)/(\pi+4)`

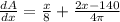
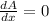
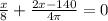
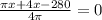
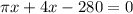
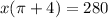
x=39.2

Again differentiate w.r.t x

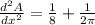`(d^2A)/(dx^2)=(1)/(8)+(1)/(2\pi)`>0

Hence, the combined area of circle and the square is minimum at x=39.2

b.When the wire is not cut and whole wire used as a circle . Then, combined area is maximum.