Question

A 432 kg merry-go-round in the shape of a horizontal disk with a radius of 2.3 m is set in motion by wrapping a rope about the rim of the disk and pulling on the rope. How large a torque would have to be exerted to bring the merry-go-round from rest to an angular speed of 3.1 rad/s in 2.1 s

Answer 1

τ = 1679.68Nm

Step-by-step explanation:

In order to calculate the required torque you first take into account the following formula:

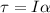`\tau=I\alpha` (1)

τ: torque

I: moment of inertia of the merry-go-round

α: angular acceleration

Next, you use the following formulas for the calculation of the angular acceleration and the moment of inertia:

`\omega=\omega_o+\alpha t` (2)

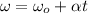`I=(1)/(2)MR^2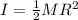` (3) (it is considered that the merry-go-round is a disk)

w: final angular speed = 3.1 rad/s

wo: initial angular speed = 0 rad/s

M: mass of the merry-go-round = 432 kg

R: radius of the merry-go-round = 2.3m

You solve the equation (2) for α. Furthermore you calculate the moment of inertia:

`\alpha=(\omega)/(t)=(3.1rad/s)/(2.1s)=1.47(rad)/(s^2)\\\\I=(1)/(2)(432kg)(2.3)^2=1142.64kg(m)/(s)`

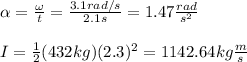
Finally, you replace the values of the moment of inertia and angular acceleration in the equation (1):

`\tau=(1142.64kgm/s)(1.47rad/s^2)=1679.68Nm`

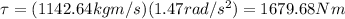
The required torque is 1679.68Nm