Question

A home improvement contractor is painting the walls and ceiling of a rectangular room. The volume of the room is 875.00 cubic feet. The cost of wall paint is $0.08 per square foot and the cost of ceiling paint is $0.14 per square foot. Find the room dimensions that result in a minimum cost for the paint.

Answer 1

The room dimensions for a minimum cost are: sides of 10 feet and height of 8.75 feet.

Explanation:

We have a rectangular room with sides x and height y.

The volume of the room is 875 cubic feet, and can be expressed as:

`V=x^2y=875`

With this equation we can define y in function of x as:

`x^2y=875\\\\y=(875)/(x^2)`

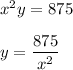
The cost of wall paint is $0.08 per square foot. We have 4 walls which have an area Aw:

`A_w=xy=x\cdot (875)/(x^2)=(875)/(x)`

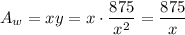
The cost of ceiling paint is $0.14 per square foot. We have only one ceiling with an area:

`A_c=x^2`

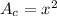
We can express the total cost of painting as:

`C=0.08\cdot (4\cdot A_w)+0.14\cdot A_c\\\\C=0.08\cdot (4\cdot (875)/(x))+0.14\cdot x^2\\\\\\C=(280)/(x)+0.14x^2`

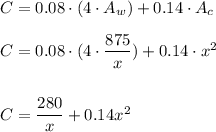
To calculate the minimum cost, we derive this function C and equal to zero:

`(dC)/(dx)=280(-1)(1)/(x^2)+0.14(2x)=0\\\\\\-(280)/(x^2)+0.28x=0\\\\\\0.28x=(280)/(x^2)\\\\\\x^3=(280)/(0.28)=1000\\\\\\x=\sqrt[3]{1000} =10`

The sides of the room have to be x=10 feet.

The height can be calculated as:

`y=875/x^2=875/(10^2)=875/100=8.75`

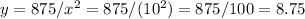
The room will have sides of 10 feet and a height of 8.75 feet.