Question

A 3.00 m-long 6.00-kg ladder pivoted at the top hangs down from a platform at the circus. A 42.0-kg trapeze artist climbs to a point where her center of mass is at the center of the ladder and swings at the system's natural frequency. What is the period of the system of ladder and woman

Answer 1

The period of the system of ladder and woman, T = 2.5 seconds

Step-by-step explanation:

Mass of the ladder,
`m_1 = 6 kg`

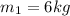
Mass of the artiste,
`m_2 = 42.0 kg`

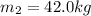
Length of the ladder, L = 42.0 kg

The total moment of inertia can be calculated using the equation:

`I = (1)/(3) M_1 L^2 + m_2 ((L)/(2) )^2\\I = (1)/(3) *6*3^2 + 42* ((3)/(2) )^2\\I = 18 + 94.5\\I = 112.5 kg m^2`

D = L/2 = 3/2

D = 1.5 m

The frequency of the system of ladder and woman follows that of a physical pendulum which can be given by the equation:

`f = (1)/(2\pi ) \sqrt{(mgD)/(I) } \\f = (1)/(2\pi ) \sqrt{(48*9.8*1.5)/(112.5) }\\f = 0.4`

The period of the system of ladder and woman is given by:

T = 1/f

T = 1/0.4

T = 2.5 seconds