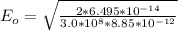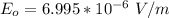Complete Question
A satellite in geostationary orbit is used to transmit data via electromagnetic radiation. The satellite is at a height of 35,000 km above the surface of the earth, and we assume it has an isotropic power output of 1 kW (although, in practice, satellite antennas transmit signals that are less powerful but more directional).
Reception devices pick up the variation in the electric field vector of the electromagnetic wave sent out by the satellite. Given the satellite specifications listed in the problem introduction, what is the amplitude E0 of the electric field vector of the satellite broadcast as measured at the surface of the earth? Use ϵ0=8.85×10^−12C/(V⋅m) for the permittivity of space and c=3.00×10^8m/s for the speed of light.
Answer:
The electric field vector of the satellite broadcast as measured at the surface of the earth is
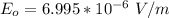
Step-by-step explanation:
From the question we are told that
The height of the satellite is
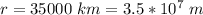
The power output of the satellite is
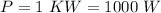
Generally the intensity of the electromagnetic radiation of the satellite at the surface of the earth is mathematically represented as
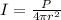
substituting values
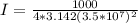
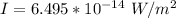
This intensity of the electromagnetic radiation of the satellite at the surface of the earth can also be mathematically represented as
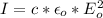
Where
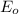 is the amplitude of the electric field vector of the satellite broadcast so
is the amplitude of the electric field vector of the satellite broadcast so
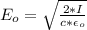
substituting values