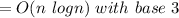Question

Consider the following modification to the Merge Sort algorithm: divide the input array into thirds (rather than halves), recursively sort each third, and finally combine the results using a three-way Merge subroutine. What is the running time of this algorithm as a function of the length n of the input array, ignoring constant factors and lower-order terms

Answer 1

The correct answer to the following question will be "n logn".

Step-by-step explanation:

• Time Complexity should be the same as the whole last particular instance, just the log base keeps changing with three.
• Throughout the circumstance of separating 2 arrays, we want one correlation. however, for splitting between 3-way arrays, will require 2 comparisons to sort.
• However, after breaking the array into 3, we can lower the number of transfers by growing the comparison. So the time complexity would then persist the same, but the log should get base 3 as we've classified into different parts.

So the time complexity will be:

⇒
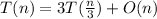
`T(n)=3T((n)/(3))+ O(n)`

⇒
`=O(n \ logn) \ with \ base \ 3`