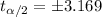Question

Suppose you will perform a test to determine whether there is sufficient evidence to support a claim of a linear correlation between two variables. Find the critical values of r given the number of pairs of data n and the significance level α. n = 12, α = 0.01

Answer 1

`t=(r √(n-2))/(√(1-r^2))`

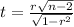
And is distributed with n-2 degreed of freedom. df=n-2=12-2=10

The significance level is
`\alpha=0.01` and
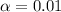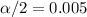`\alpha/2 = 0.005` and for this case we can find the critical values and we got:

`t_(\alpha/2)= \pm  3.169`

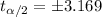
Explanation:

In order to test the hypothesis if the correlation coefficient it's significant we have the following hypothesis:

Null hypothesis:
`\rho =0`

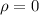
Alternative hypothesis:
`\rho \\eq 0`

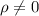
The statistic to check the hypothesis is given by:

`t=(r √(n-2))/(√(1-r^2))`

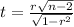
And is distributed with n-2 degreed of freedom. df=n-2=12-2=10

The significance level is
`\alpha=0.01` and
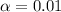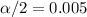`\alpha/2 = 0.005` and for this case we can find the critical values and we got:

`t_(\alpha/2)= \pm  3.169`