Question

A 0.260 m radius, 525 turn coil is rotated one-fourth of a revolution in 4.17 ms, originally having its plane perpendicular to a uniform magnetic field. (This is 60 rev/s.) Find the magnetic field strength needed to induce an average emf of 10,000 V.

Answer 1

B = 0.37T

Step-by-step explanation:

In order to calculate the needed magnitude of the magnetic force you use the following formula, which calculate the induced emf of the solenoid when there is a change in the magnetic flux:

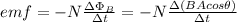`emf=-N(\Delta \Phi_B)/(\Delta t)=-N(\Delta (BAcos\theta))/(\Delta t)` (1)

emf: induced voltage in the solenoid = 10,000V

N: turns of the solenoid = 525

ФB: magnetic flux

B: magnitude of the magnetic field = ?

A: cross-sectional area of the solenoid = π*r^2

r: radius of the cross-sectional area = 0.260m

Δt: interval time of the change of the magnetic flux = 4.17ms = 4.17*10^-3s

First, you have the magnetic field direction perpendicular to the plane of the solenoid, after, the angle between them is 90° (quarter of a revolution)

In the equation (1) the only parameter that changes on time is the angle, then, you can solve for B from the equation (1):

`emf=-NBA(cos(90\°)-cos(0\°))/(\Delta t)=(NBA)/(\Delta t)\\\\B=((\Delta t)(emf))/(NA)=((\Delta t)(emf))/(N(\pi r^2))\\\\`

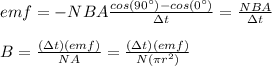
Finally, you replace the values of the parameters to calculate B:

`B=((4.17*10^(-3)s)(10000V))/((525)(\pi(0.260m)^2))=0.37T`

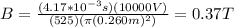
The strength of the magnetic field is 0.37T