Question

Consider the functions f (x )equals negative 9 x plus 3 and g (x )equals negative one ninth (x minus 3 ). ​(a) Find​ f(g(x)). ​(b) Find​ g(f(x)). ​(c) Determine whether the functions f and g are inverses of each other.

Answer 1

`(a) f(g(x)) = x\\(b) g(f(x)) = x`

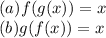
(c) Yes, the functions f and g are inverses of each other.

Explanation:

Given the functions:

`f(x) = -9x+3\\g(x) = -(1)/(9)(x-3)`

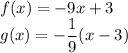
(a)
`f(g(x))=?`

`put\ x = -(1)/(9)(x-3)\ in\ (-9x+3):`

`f(g(x))= -9(-(1)/(9)(x-3)) +3\\\Rightarrow (-(-9)/(9)(x-3)) +3\\\Rightarrow ((9)/(9)(x-3)) +3\\\Rightarrow 1(x-3) +3\\\Rightarrow x-3 +3\\\Rightarrow x\\\Rightarrow f(g(x) )=x`

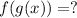
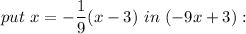
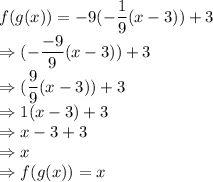
(b)
`g(f(x))=?`

`put\ x = (-9x+3)\ in\ -(1)/(9)(x-3):`

`f(g(x))= (-(1)/(9)((-9x+3)-3))\\\Rightarrow (-(1)/(9)(-9x+3-3))\\\Rightarrow (-(1)/(9)(-9x))\\\Rightarrow (-(-9)/(9)x)\\\Rightarrow g(f(x))=x`

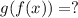
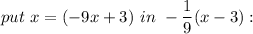
(c) Yes, f and g are the inverse functions of each other.

As per the property of inverse function:

If
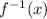`f^(-1)(x)` is the inverse of
`f(x)` then:

`f(f^(-1)(x)) = x`

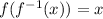
And here, we have the following as true:

`f(g(x)) = x\\ g(f(x)) = x`

`\therefore` f and g are inverse functions of each other.