Question

Water at 70 kPa flows through a horizontal 2 meter diameter pipe at a velocity of 71 m/s and an elevation of 54 meters. If the density of water is 1000 kg/m^3 and the specific weight is 9.8 kN/m^3, what is the total pressure? Round to the nearest kPa.

Answer 1

The total pressure is 3120 kilopascals.

Step-by-step explanation:

The total pressure of this water flow is determined by the Bernoulli's Principle, which is the sum of dynamic (
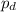`p_(d)`) and hydraulic pressure (
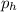`p_(h)`). That is:

`p_(T) = p_(d) + p_(h)`

`p_(T) = (1)/(2)\cdot \rho \cdot v^(2) + \gamma \cdot z + p`

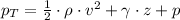
Where:

`\rho` - Density, measured in kilograms per cubic meter.

`v` - Flow velocity, measured in meters per second.

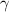`\gamma` - Specific weight, measured in newtons per cubic meter.

`z` - Elevation, measured in meters.

`p` - Static pressure, measured in pascals.

Given that
`\rho = 1000\,(kg)/(m^(3))`,
`v = 71\,(m)/(s)`,
`\gamma = 9800\,(N)/(m^(3))`,
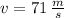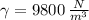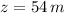`z = 54\,m` and
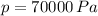`p = 70000\,Pa`, the total pressure is:

`p_(T) = (1)/(2)\cdot \left(1000\,(kg)/(m^(3)) \right)\cdot \left(71\,(m)/(s) \right)^(2) + \left(9800\,(N)/(m^(3)) \right)\cdot (54\,m)+70000\,Pa`

`p_(T) = 3119700\,Pa`

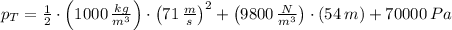
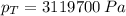
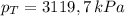`p_(T) = 3119,7\,kPa` (1 kPa = 1000 Pa)

`p_(T) = 3120\,kPa`

The total pressure is 3120 kilopascals.