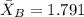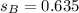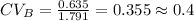Answer:
Dataset A
We have the following results:
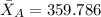
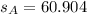

Dataset B
We have the following results:
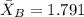
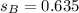
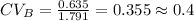
Explanation:
For this case we have the following info given:
A: 431, 447, 306, 413, 315, 432, 312, 387, 295, 327, 323, 296, 441, 312
B: $1.35, $1.82, $1.82, $2.72, $1.07, $1.86, $2.71, $2.61, $1.13, $1.20, $1.41
We need to remember that the coeffcient of variation is given by this formula:
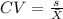
Where the sample mean is given by:
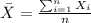
And the sample deviation given by:
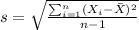
Dataset A
We have the following results:
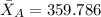
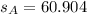

Dataset B
We have the following results: