Answer:
The random variable (number of toppings ordered on a large pizza) has a mean of 1.14 and a standard deviation of 1.04.
Explanation:
The question is incomplete:
The probability distribution is:
x P(x)
0 0.30
1 0.40
2 0.20
3 0.06
4 0.04
The mean can be calculated as:
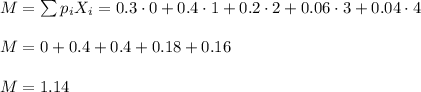
(pi is the probability of each class, Xi is the number of topping in each class)
The standard deviation is calculated as:
