Question

You find 20 coins consisting only of nickels, dimes, and quarters, with a face value of $2.65. However, the coins all date from 1929, and are worth considerably more than their face value. A coin dealer offers you $7 for each nickel, $5 for each dime, and $20 for each quarter, for a total of $221. How many of each type of coin did you find

Answer 1

8 nickels, 5 dimes and 7 quarters

Explanation:

Each nickel is $0.05, each dime is $0.10 and each quarter is $0.25.

So, if we have n nickes, d dimes and q quarters, we can write the system of equations:

`n + d + q = 20\ (eq1)`

`0.05n + 0.1d + 0.25q = 2.65\ (eq2)`

`7n + 5d + 20q = 221\ (eq3)`

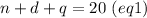
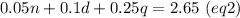
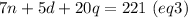
If we multiply (eq2) by 140 and (eq1) by 7, we have:

`7n + 14d + 35q = 371\ (eq4)`

`7n + 7d + 7q = 140\ (eq5)`

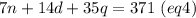
Now, making (eq4) - (eq3) and (eq5) - (eq3), we have:

`9d + 15q = 150\ (eq6)`

`2d - 13q = -81\ (eq7)`

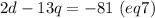
Multiplying (eq7) by 4.5, we have:

`9d - 58.5q = -364.5\ (eq8)`

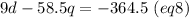
Subtracting (eq6) by (eq8), we have:

`73.5q = 514.5`

`q = 7`

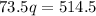
Finding 'd' using (eq6), we have:

`9d + 15*7 = 150`

`9d = 150 - 105`

`d = 5`

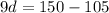
Finding 'n' using (eq1), we have:

`n + 5 + 7 = 20`

`n = 8`

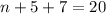
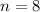
So we have 8 nickels, 5 dimes and 7 quarters.