Question

A steel wire with mass 25.3 g and length 1.62 m is strung on a bass so that the distance from the nut to the bridge is 1.10 m. (a) Compute the linear density of the string. kg/m (b) What velocity wave on the string will produce the desired fundamental frequency of the E1 string, 41.2 Hz

Answer 1

(a) μ = 0.015kg/m

(b) v = 90.64m/s

Step-by-step explanation:

(a) The linear density of the string is given by the following relation:

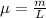`\mu=(m)/(L)` (1)

m: mass of the string = 25.3g = 25.3*10-3 kg

L: length of the string = 1.62m

`\mu=(25.3*10^(-3)kg)/(1.62m)=0.015(kg)/(m)`

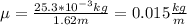
The linear density of the string is 0.015kg/m

(b) The velocity of the string for the fundamental frequency is:

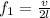`f_1=(v)/(2l)` (2)

f1: fundamental frequency = 41.2 Hz

vs: speed of the wave

l: distance between the fixed extremes of the string = 1.10m

You solve for v in the equation (2) and replace the values of the other parameters:

`v=2lf_1=2(1.10m)(41.2Hz)=90.64(m)/(s)`

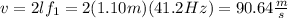
The speed of the wave for the fundamental frequency is 90.64m/s