Question

A particle with positive charge q = 2.72 10-18 C moves with a velocity v with arrow = (5î + 4ĵ − k) m/s through a region where both a uniform magnetic field and a uniform electric field exist. (a) Calculate the total force on the moving particle, taking B with arrow = (3î + 3ĵ + k) T and E with arrow = (2î − ĵ − 5k) V/m.

Answer 1

`F = 10^(-18) *(24.48i + 24.48j - 5.44k)`

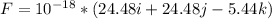
Step-by-step explanation:

The charge, q, of the particle is
`2.72 * 10^(-18) C`

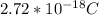
The velocity, v, of the particle is (5i + 4j - k) m/s

It moves in a region containing electric field, E, of (2i - j - 5k) V/m and magnetic field, B, of (3i + 3j + k) T.

The electric force acting on the particle is given as:

`F = q[E + (v X B)]`

where v X B is cross product.

Therefore:

`F = 2.72 * 10^(-18) * [(2i - j - 5k) + ((5i + 4j - k) X (3i + 3j + k))`

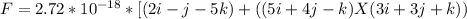
Let us solve (5i + 4j - k) X (3i + 3j + k):

`\left[\begin{array}{ccc}i&j&k\\5&4&-1\\3&3&1\end{array}\right]`

i(4 + 3) - j(5 + 3) + k(15 - 12) = 7i - 8j + 3k

Therefore:

`F = 2.72 * 10^(-18) * [(2i - j - 5k) + (7i - 8j + 3k)]\\\\F = 2.72 * 10^(-18) *(9i -9j -2k) N\\\\F = 10^(-18) *(24.48i + 24.48j - 5.44k)`