Question

Male players at the high school, college, and professional ranks use a regulation basketball that weighs 22.0 ounces with a standard deviation of 1.2 ounces. Assume that the weights of basketballs are approximately normally distributed. If a basketball is randomly selected, what is the probability that it will weigh between 21.4 and 23.8 ounces

Answer 1

The probability that a basketball will weigh between 21.4 and 23.8 ounces is 0.62465.

Explanation:

We have all this information from the question:

• The weights of the basketballs are approximately normally distributed.
• The population mean,
  `\\ \mu`, for basketball weights is 22.0 ounces,
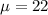  `\\ \mu = 22` ounces.
• The population standard deviation,
  `\\ \sigma`, for basketball weights is 1.2 ounces,
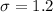  `\\ \sigma = 1.2` ounces.

To answer this question:

• First, we need to calculate the cumulative probability for
  `\\ x = 21.4` ounces and
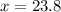  `\\x = 23.8` ounces.
• Second, subtract both values to obtain the asked probability, that is the probability that [a basketball] will weigh between 21.4 and 23.8 ounces.

Important concepts to remember:

For this, it is crucial three concepts: the standard normal distribution, the standard normal table, and z-scores:

Roughly speaking, the standard normal distribution is a normal distribution for standardized values. We can obtain standardized values using the formula for z-scores:

`\\ z = (x - \mu)/(\sigma)` [1]

And these values represent the distance from the population mean in standard deviation units. When they are positive, these values are above the population mean,
`\\ \mu`. In case they are negative, they are below
`\\ \mu`.

We can obtain probabilities for any normally distributed data using the standard normal distribution. These values are tabulated into the standard normal table, available in Statistics books or on the Internet.

In general, these values are cumulative probabilities, that is, probabilities from
`\\ -\infty` to the value x in question (a raw value).

At this stage, we have enough information to solve the question.

Solving the question

Cumulative probability for
`\\ P(X<21.4)` ounces.

• Obtain the z-score, using [1], for
  `\\ x = 21.4` ounces (without using units):

`\\ z = (x - \mu)/(\sigma)`

`\\ z = (21.4 - 22)/(1.2)`

`\\ z = (-0.6)/(1.2)`

`\\ z = -0.5`

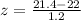
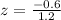
That is, the raw score
`\\ x = 21.4` is 0.5 standard deviations below,
`\\ z = -0.5`, the population mean.

• Getting
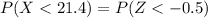  `\\ P(X<21.4) = P(Z<-0.5)` using the standard normal table.

Since
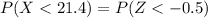`\\ P(X<21.4) = P(Z<-0.5)`, we can consult the standard normal table, using
`\\ z = -0.5` as an entry (using its first column).

The first row of this table has a second digit in the decimal part for the value of z. In this case, this second digit is zero (or to be more precise, -0.00), because
`\\ z = -0.50`. With the intersection of these two values in the table, namely, -0.5 and -0.00, we finally obtain the cumulative probability,
`\\ P(Z<-0.50) = 0.30854`.

Thus,
`\\ P(X<21.4) = P(Z<-0.50) = 0.30854`

Cumulative probability for
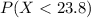`\\ P(X<23.8)` ounces.

We can follow the same steps as before:

`\\ z = (x - \mu)/(\sigma)`

`\\ z = (23.8 - 22.0)/(1.2)`

`\\ z = (1.8)/(1.2)`

`\\ z = 1.5`

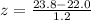
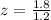
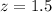
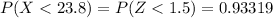`\\ P(X<23.8) = P(Z<1.5) = 0.93319` using the standard normal table (z =1.5, +0.00).

Therefore,
`\\ P(X<23.8) = P(Z<1.5) = 0.93319`

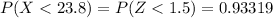
Then, to answer the probability that a basketball will weigh between 21.4 and 23.8 ounces, we subtract (as we mentioned before) both cumulative probabilities:

`\\ P(21.4 < X < 23.8) = P(-0.5 < Z < 1.5) = P(X<23.8) - P(X<21.4) = P(Z<1.5) - P(Z<-0.5) = 0.93319 - 0.30854 = 0.62465`

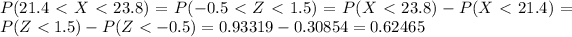
Then, the probability that a basketball will weigh between 21.4 and 23.8 ounces is 0.62465.

We can see this probability represented by the shaded area in the below graph.