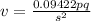Answer:
Mathematical model =
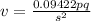
k = 0.09422
Explanation:
If v varies jointly as p and q, this means that v varies directly as the product of p and q as shown;
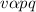
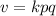 ... 1
... 1
k = constant of proportionality
Also v varies inversely as the square of s; mathematically,
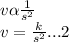
Equating 1 and 2, we have;
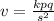
Given v = 1.6, when p=4.1, q=7 and s=1.3
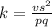
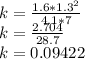
The constant of proportionality is 0.09422
The expression therefore becomes