Answer:
The length of a 95% confidence interval for mean Age is 3.72.
Explanation:
The data is provided for the age of 100 adults.
The mean and standard deviation are:
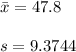
As the sample size is too large the z-interval will be used for the 95% confidence interval for mean.
The critical value of z for 95% confidence level is, z = 1.96.
The length of a confidence interval is given by:
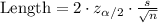
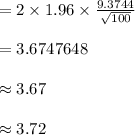
Thus, the length of a 95% confidence interval for mean Age is 3.72.