Answer:
Explanation:
The main idea is that I would like to pay less than what I'm expecting to win, so in that way, I get a profit out of playing this game. Let X be the number of tosses until I get a Heads. By definition, this is a geometric random variable with parameter p = 1/2.
Let Y the amount I received for playing. So, we want to calculate the expected value of Y.
We can calculate it as follows
![E[Y] = 2 P(X=1)+ 4 P(X=2)+ 8 P(X =3) + \dots = \sum_(n=1)^infty 2^n P(X=n)](https://img.qammunity.org/2021/formulas/mathematics/college/peg2eeawvg4hud4f029ubgh486121hiwa2.png)
Since X is a geometric random variable, we have that
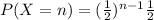
Then,
![E[Y] = \sum_(n=1)^\infty 2^(n) ((1)/(2))^(n-1) (1)/(2) = \sum_(n=1)^\infty 2^(n-1) \cdot (1)/(2^(n-1)) = \sum_(n=1)^\infty 1 = \infty](https://img.qammunity.org/2021/formulas/mathematics/college/8r5rkzp1g4zt50xopa7f0fkx7z7y2l4oa6.png)
So, we expect to have an infinite amount. Given this, we can pay as much as we want to play the game.