Question

The goalkeeper of the USA ice hockey National Team, Jonathan Quick, saved 91.6% of shots during his entire career in the NHL. Estimate the probability that he let through more than 2 goals if the opposite team made 60 shots on goal.

Answer 1

88.93% probability that he let through more than 2 goals if the opposite team made 60 shots on goal.

Explanation:

For each shot, there are only two possible outcomes. Either he lets it through, or he does not. Shots are independent. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

The goalkeeper of the USA ice hockey National Team, Jonathan Quick, saved 91.6% of shots during his entire career in the NHL.

So he let in a goal in 100 - 91.6 = 8.4% of the shots, so
`p = 0.084`

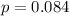
60 shots:

This means that
`n = 60`

Estimate the probability that he let through more than 2 goals if the opposite team made 60 shots on goal.

Either he lets two or less goals, or he lets more than 2. The sum of the probabilities of these outcomes is 1. So

`P(X \leq 2) + P(X > 2) = 1`

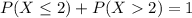
We want
`P(X > 2)`.

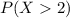Then

`P(X > 2) = 1 - P(X \leq 2)`

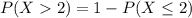
In which

`P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(60,0).(0.084)^(0).(0.916)^(60) = 0.0052`

`P(X = 1) = C_(60,1).(0.084)^(1).(0.916)^(59) = 0.0285`

`P(X = 2) = C_(60,2).(0.084)^(2).(0.916)^(58) = 0.0770`

`P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0.0052 + 0.0285 + 0.0770 = 0.1107`

`P(X > 2) = 1 - P(X \leq 2) = 1 - 0.1107 = 0.8893`

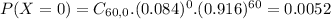
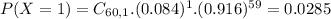
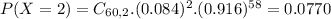
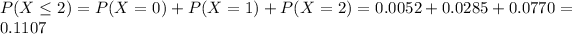
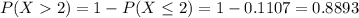
88.93% probability that he let through more than 2 goals if the opposite team made 60 shots on goal.