Answer:
0.9 = 90%
Step-by-step explanation:
An uniform probability is a case of probability in which each outcome is equally as likely.
For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.
The probability that we find a value X between c and d is given by the following formula.
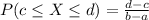
Miles per gallon of a vehicle is a random variable with a uniform distribution from 25 to 35.
This means that
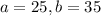
The probability that a random vehicle gets between 25 and 34 miles per gallon is:
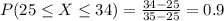
So the answer is 0.9 = 90%