Question

In △ABC, point P∈AC with AP:PC=1:3, point Q∈AB so that AQ:QB=3:4, Find the ratios A(PBQ) : A(PBC) and A(AQP) : A(ABC)

Answer 1

The ratio APBQ : APBC is 4:21, AAQP : AABC is 3:28

Explanation:

Data provided in the question

AP : PC = 1 : 3

So let us assume AP = x and PC = 3x.

And, If AQ : QB = 3 : 4

So, let us assume AQ = 3y and QB = 4y.

Now we have to find the area of ΔAQP and ΔABC

`A_(AQP)=(1)/(2)\cdot AP\cdot AQ\cdot \sin\angle A=(1)/(2)\cdot x\cdot 3y\cdot \sin\angle A;`

`A_(ABC)=(1)/(2)\cdot AC\cdot AB\cdot \sin\angle A=(1)/(2)\cdot (x+3x)\cdot (3y+4y)\cdot \sin\angle A=(1)/(2)\cdot 4x\cdot 7y\cdot \sin\angleA`

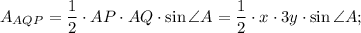
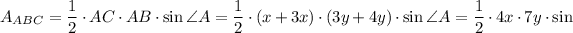
Therefore

`(A_(APQ))/(A_(ABC))=((1)/(2)\cdot x\cdot 3y\cdot \sin\angle A)/((1)/(2)\cdot 4x\cdot 7y\cdot \sin\angleA)=(3)/(28).`

Now

`(A_(APQ))/(A_(ABP))=((1)/(2)\cdot x\cdot 3y\cdot \sin\angle A)/((1)/(2)\cdot x\cdot (3y+4y)\cdot \sin\angle A)=(3)/(7).`

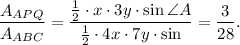
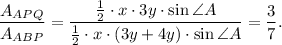
Now after solving these two ratios we can find

`A_(ABP)=(7)/(3)A_(APQ)\Rightarrow A_(PBQ)=A_(APB)-A_(APQ)=(7)/(3)A_(APQ)-A_(APQ)=(4)/(3)A_(APQ)`

`A_(ABC)=(28)/(3)A_(APQ)\Rightarrow A_(PBC)=A_(ABC)-A_(APB)=(28)/(3)A_(APQ)-(7)/(3)A_(APQ)=7A_(APQ).`

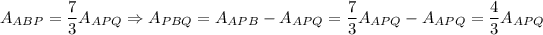
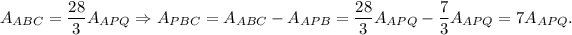
Therefore

`(A_(PBQ))/(A_(PBC))=((4)/(3)A_(APQ))/(7A_(APQ))=(4)/(21).`

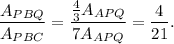
Hence, we applied the above equation so that we can get to know the ratios