Question

The difference of the degrees of the polynomials p(x) = 3x2y2 + 5xy? - x6 and q(x) = 3x5 - 4x3 + 2 is

(A) 5
(B) 9
(C) 2.
(D) 3​

Answer 1

The difference of the degrees of the polynomials p (x) and q (x) is 1.

Explanation:

A polynomial function is made up of two or more algebraic terms, such as p (x), p (x, y) or p (x, y, z) and so on.

The polynomial’s degree is the highest exponent or power of the variable in the polynomial function.

The polynomials provided are:

`p(x) = 3x^(2)y^(2) + 5xy - x^(6)\\\\q(x) = 3x^(5) - 4x^(3) + 2`

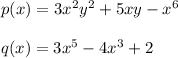
The degree of polynomial p (x) is:

`\text{deg}\ p (x)=6`

The degree of polynomial q (x) is:

`\text{deg}\ q (x)=5`

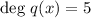
The difference of the degrees of the polynomials p (x) and q (x) is:

`\text{deg}\ p(x)-\text{deg}\ q(x)=6-5=1`

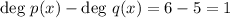
Thus, the difference of the degrees of the polynomials p (x) and q (x) is 1.