Question

Which rate can you set StartFraction 30 miles Over 1 hour EndFraction equal to in order to find the time it takes to travel 900 miles at 30 miles per hour?

Answer 1

the answer is:

d. 900/? hours

Answer 2

`\frac{30\,\text{mi}}{1\,\text{h}}=\frac{900\,\text{mi}}{t}`

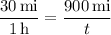
Explanation:

Since you have miles in the numerator of your rate, you need miles in the numerator of the equivalent fraction:

`\frac{30\,\text{mi}}{1\,\text{h}}=\frac{900\,\text{mi}}{t}`

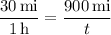
This can be rearranged to ...

`\frac{t}{1\,\text{h}}=\frac{900\,\text{mi}}{30\,\text{mi}}=30`

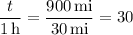
Then, multiplying by 1 h gives the solution ...

t = 30 h

It takes 30 hours to travel 900 miles at 30 miles per hour.