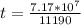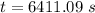Answer:
a
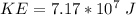
b
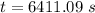
Step-by-step explanation:
From the question we are told that
The radius of the flywheel is
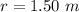
The mass of the flywheel is

The rotational speed of the flywheel is
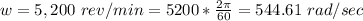
The power supplied by the motor is
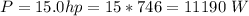
Generally the moment of inertia of the flywheel is mathematically represented as
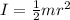
substituting values
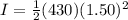

The kinetic energy that is been stored is
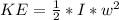
substituting values
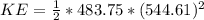
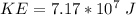
Generally power is mathematically represented as
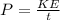
=>
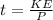
substituting the value