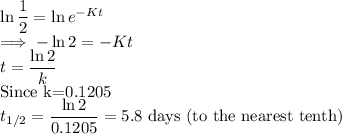Question

A 25 gram sample of a substance that's used for drug research has a k-value of 0.1205. Find the substance's half life in days, round to the nearest tenth.

Answer 1

Complete Question

Situation: A 25 gram sample of a substance used for drug research has a k-value of 0.1205.
`N=N_0e^-kt`

• 
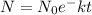
  `N_0`= initial mass(at time t=0)
• N= mass at a time t
• K= a positive constant that depends on the substance itself and on the units used to measure time
• T=time, in days

Find the substance's half-life in days, round to the nearest tenth.

Answer:

5.8 days

Explanation:

The decay model for drugs and radioactive substances is given as

`N=N_0e^(-Kt)`

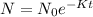
The half-life of any substance is the time it takes for the substance to decay to half its initial amount. That is the period it takes for:

`N(t)=(N_0)/(2)`

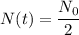
If we substitute this into the model, we obtain:

`(N_0)/(2)=N_0e^(-Kt)\\$Dividing both sides by N_o\\\frac12=e^(-Kt)`

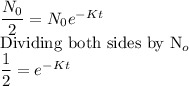
We can solve for t.

Taking the natural logarithm of both sides

`\ln\frac12=\ln e^(-Kt)\\\implies-\ln2=-Kt\\t=(\ln2)/(k) \\$Since k=0.1205$\\t_(1/2)=(\ln2)/(0.1205)=5.8$ days (to the nearest tenth)`